Module 5 Answer Key
5.7 Exercises
A. Credit Assessment of All-Weather
1.
Struthers should approve All-Weather’s application for a 3-year term loan. The company’s debt service cover ratio (DSCR) barely meets the bank’s minimum requirement now, but it is expected to improve over the term of the loan as industry conditions improve according to the pro forma financial statements prepared by Struthers. If All-Weather does experience difficulties, sufficient high-quality collateral and a personal guarantee from the owner should ensure payment.
Based on Struthers’ pro forma financial ratios, All-Weather should have a credit score of 5. Given its excellent credit history, the quality of its collateral, the personal guarantee provided by its owner, strong industry growth prospects, and improving company performance, All-Weather should be given a one-step increase in its credit score to 4. An interest rate of 6.20% (prime plus 120 bps) should be negotiated.
B. Capitalizing Leases at Secure Transport
1.
[latex](10)(2,263.19)=22,631.90[/latex]
[latex]22,631.90+22,631.90(\frac{{1-(1+(\frac{{.09}}{{12}}))^{-119}}}{{(\frac{{.09}}{{12}})}})=1,800,000[/latex]
These are annuities due – the first lease payment is made at delivery, that is at the beginning of the month, not the end, so no interest is paid on this payment. This is the reason 119 is used in the annuity calculation above instead of 120.
[latex]\frac{{1,800,000}}{{((10)(180,000))}}=1.00{\text{ or }}100{\text{%}}[/latex]
This step relates to the terminal value of the lease. If you compare this question to the next problem, C, where the stuff being leased has a terminal value, you will see why this is being done. It is the percentage of the stuff being used up from the lessors’ point of view during the lease.
| Period | Beginning Balance | Payment | Interest | Ending Balance |
| 1 | 1,800,000.00 | 22,631.90 | 13,330.26 | 1,790,698.36 |
Income Statement
| Interest expense | 13,330.26 | |
| Depreciation expense1 | 10,000.00 |
To calculate the interest expense, you could build an amortization table, or you could just find the difference in value between the 1st and 2nd month. If you are using a financial calculator, set it to beginning to accommodate the annuity due. Enter 1,800,000 as the PV. If there was value at the end of the lease you would enter it as a negative cash flow for FV. Enter 9/12 or 0.75 as i/y, enter 120 as N and then solve for payment. You should get 22,631.90. Now enter 1 as N and solve for FV and you will get 1,790,698.36 which is your obligation under the capital lease. The difference between 1,800,000 and 1,790,698.36 is 9301.64 which is the principal reduction. Subtract this from the payment of 22,631.9 to get 13,330.26 which is the interest paid.
Property, Plant and Equipment
| Equipment held under capital lease | 1,800,000.00 | |
| Less: Accumulative deprecation | 10,000.00 | |
| Net equipment held under capital lease | 1,790,000.00 |
Current Liabilities
| Obligation under capital lease | 117,204.62 |
Long-term Liabilities
| Obligation under capital lease | 1,790,689.36 | |
| Less: Current portion | 117,204.62 | |
| Net obligation2 | 1,673,484.74 |
[latex]^{1}\frac{{1,800,000}}{{(15{\text{x}}12}}[/latex]
[latex]^{2}22,631.90+22,631.90(\frac{{1-(1+(\frac{{.09}}{{12}}))^{-106}}}{{(\frac{{.09}}{{12}})}})[/latex]
This too relates to the annuity due. The 22,631.9 is the payment due at the very beginning of the year, and the 106 payments are the remainder that are due from then on. 119 – 12 – 1 = 106, or put another way, 106 payments due in future, plus 1 due now (1 year from today) is the original number of payments less 1 year.
Note: The asset is depreciated over 15 years because the company is taking possession of it at the end of the lease for CAD 0.00 as part of a bargain purchase option. The present value of the lease payments equal the full value of the asset.
C. Capitalizing Leases at Wilson
1.
[latex](2)(1,754.88)=3,509.76[/latex]
[latex]3,509.76+3,509.76(\frac{{1-(1+(\frac{{.08}}{{12}}))^{-59}}}{{(\frac{{.08}}{{12}})}})=174,249.84[/latex]
[latex]\frac{{174,249.84}}{{((2)(95,000))}}=.92[/latex]
| Period | Beginning Balance | Payment | Interest | Ending Balance |
| 1 | 174,249.84 | 3,509.76 | 1,138.27 | 171,878.35 |
Income Statement
| Interest expense | 1,138.27 | |
| Depreciation expense1 | 2,904.16 |
Property, Plant and Equipment
| Equipment held under capital lease | 174,249.84 | |
| Less: Accumulative deprecation | 2,904.16 | |
| Net equipment held under capital lease | 171,345.68 |
Current Liabilities
| Obligation under capital lease | 29,721.75 |
Long-term Liabilities
| Obligation under capital lease | 171,878.35 | |
| Less: Current portion | 29,721.75 | |
| Net obligation2 | 142,156.60 |
[latex]^{1}\frac{{174,249.84}}{{(15{\text{x}}12}}[/latex]
[latex]^{2}3,509.76+3,509.76(\frac{{1-(1+(\frac{{.08}}{{12}}))^{-46}}}{{(\frac{{.08}}{{12}})}})[/latex]
Note: The asset is depreciated over 5 years because that is the lease term and the lessee is returning the asset at that time. The present value of the lease payments equals the value of the leased assets relating to the term of the lease only.
D. Capitalizing Leases at Porta Power
1.
[latex](4)(3,585.97)=14,343.88[/latex]
[latex]14,343.88+14,343.88(\frac{{1-(1+(\frac{{.10}}{{12}}))^{-95}}}{{(\frac{{.10}}{{12}})}})=953,160.40[/latex]
[latex]\frac{{953,160.40}}{{((4)(238,300))}}=1.00{\text{ or }}100{\text{%}}[/latex]
| Period | Beginning Balance | Payment | Interest | Ending Balance |
| 1 | 953,160.40 | 14,343.88 | 7,823.47 | 946,639.99 |
Income Statement
| Interest expense | 7,823.47 | |
| Depreciation expense1 | 7,943.00 |
Property, Plant and Equipment
| Equipment held under capital lease | 953,160.40 | |
| Less: Accumulative deprecation | 7,943.00 | |
| Net equipment held under capital lease | 945,217.40 |
Current Liabilities
| Obligation under capital lease | 82,615.41 |
Long-term Liabilities
| Obligation under capital lease | 946,639.99 | |
| Less: Current portion | 82,615.41 | |
| Net obligation2 | 864,024.58 |
[latex]^{1}\frac{{953,160.40}}{{(10{\text{x}}12}}[/latex]
[latex]^{2}14,343.88+14,343.88(\frac{{1-(1+(\frac{{.10}}{{12}}))^{-82}}}{{(\frac{{.10}}{{12}})}})[/latex]
E. Capitalizing Leases at Acme
1.
[latex]2,000+2,000(\frac{{1-(1+(\frac{{.05}}{{12}}))^{-23}}}{{(\frac{{.05}}{{12}})}})=45,777.75[/latex]
| Period | Beginning Balance | Payment | Interest | Ending Balance |
| 1 | 45,777.75 | 2,000.00 | 182.41 | 43,960.16 |
Income Statement
| Interest expense | 182.41 | |
| Depreciation expense1 | 1,907.41 |
Property, Plant and Equipment
| Equipment held under capital lease | 45,777.75 | |
| Less: Accumulative deprecation | 1,907.41 | |
| Net equipment held under capital lease | 43,870.34 |
Current Liabilities
| Obligation under capital lease | 22,410.96 |
Long-term Liabilities
| Obligation under capital lease | 43,960.16 | |
| Less: Current portion | 22,410.96 | |
| Net obligation2 | 21,549.20 |
[latex]^{1}\frac{{45,777.75}}{{(2{\text{x}}12)}}[/latex]
[latex]^{2}2,000+2,000(\frac{{1-(1+(\frac{{.05}}{{12}}))^{-10}}}{{(\frac{{.05}}{{12}})}})[/latex]
Note: The incremental borrowing rate was used because the rate implicit in the lease was not available.
F. Calculating Lease Payments at Stead Leasing
See the section in the readings called TAX LAW
See the section on calculating lease payments. These formulas follow directly.
1.
Value of asset – Present value of CCA tax shield = Present value of after-tax lease payments + Present value of residual value.
Value of asset – Present Value of CCA tax shield = [latex]5,000,000 - 5,000,000\left( {.3} \right)\left( {\frac{{.3}}{{.3 + .12}}} \right)\left( {\frac{{2 + .12}}{{2\left( {1 + .12} \right)}}} \right)[/latex]
The Present Value of after-tax lease payments = [latex]\left( {1 - .3} \right)\left( {P + P\left( {\frac{{1 - {{\left( {1 + .01} \right)}^{ - 119}}}}{{.01}}} \right)} \right)[/latex]
The Present Value of residual value = [latex]\frac{{1,000,000}}{{{{\left( {1 + .01} \right)}^{120}}}} - \frac{{\left( {1,000,000} \right)\left( {.3} \right)\left( {\frac{{.30}}{{.30 + .12}}} \right)\left( {\frac{{2 + .12}}{{2\left( {1 + .12} \right)}}} \right)}}{{{{\left( {1 + .01} \right)}^{120}}}}[/latex]
where the 2nd term is the PV of the tax shield on the salvage value. (Note: see the formula sheet for this version of the 1/2 year rule formula.)
Finally, solve for P using algebra (see the Excel spreadsheet)
[latex]\begin{array}{rcl}5,000,000-(5,000,000)(.3)(\frac{{.3}}{{.3+.12}})(\frac{{2+.12}}{{2(1+.12)}})&=&(1-.3)({\text{P}}+{\text{P}}(\frac{{1-(1+.01)^{-119}}}{{.01}}))+\frac{{1,000,000}}{{(1+.01)^{120}}}-\frac{{(1,000,000)(.3)(\frac{{.30}}{{.30+.12}})(\frac{{2+.12}}{{2(1+.12)}})}}{{(1+.01)^{120}}}\\{\text{P}}&=&{\text{CAD }}75,985.29\end{array}[/latex]
2.
[latex]\begin{array}{rcl}5,000,000-(5,000,000)(.3)(\frac{{.3}}{{.3+i}})(\frac{{2+.i}}{{2(1+i)}})&=&(1-.3)(82,000+82,000(\frac{{1-(1+(\frac{{i}}{{12}}))^{-119}}}{{(\frac{{i}}{{12}})}}))+\frac{{1,000,000}}{{(1+(\frac{{i}}{{12}}))^{120}}}-\frac{{(1,000,000)(.3)(\frac{{.30}}{{.30+i}})(\frac{{2+i}}{{2(1+i)}})}}{{(1+(\frac{{i}}{{12}}))^{120}}}\\i&=&13.48{\text{%}}\end{array}[/latex]
You must use goal seek or solver in Excel to solve for the interest rate, i. There is no closed form solution. The only other option is to guess a value for i, solve the equation, try another value for I, and repeat until you are close.
3.
[latex]\begin{array}{rcl}5,000,000-(5,000,000)(.3)(\frac{{.3}}{{.3+.12}})(\frac{{2+.12}}{{2(1+.12)}})&=&(1-.3)({\text{P}}+{\text{P}}(\frac{{1-(1+.01)^{-119}}}{{.01}}))+\frac{{1,000,000}}{{(1+.01)^{120}}}-\frac{{(1)(.3)(\frac{{.30}}{{.30+.12}})(\frac{{2+.12}}{{2(1+.12)}})}}{{(1+.01)^{120}}}\\{\text{P}}&=&{\text{CAD }}80,886.96\end{array}[/latex]
Note: Compared to Part 1, the lease payments are higher because the lessee is paying for the full value of the asset over the lease term.
G. Lease or Buy at Hawkeye
1.
Lease? No – purchase with a bank loan
| Present value of loan payments1 | 3,000.00 |
| Present value of lost CCA tax shield2 | (595.82) |
| Present value of lease payments3 | (2,560.66) |
| Total | (156.48) |
For tax purposes, you get to deduct the interest expense, but also the taxable depreciation of the item, which is the CCA. As long as the company has any items in the same CCA category as the item under consideration, the CCA does not change whether or not the company still has the item, so in this case, they use the machine for 3 years but depreciate it over many more. Each year the depreciation saves the company from paying taxes. The present value of the tax shield is the value today of all these tax savings over the years the item is depreciated.
Note: Other qualitative advantages of leasing may still cause the company to select this more costly option. See the Excel file to see how the values in these tables were calculated.
1
| Year | Principal | Interest
(11.2%) |
Tax Savings
(.25) |
After-tax Cost of Buying | Present Value (8.40%) |
| 1 | (1,000) | (336) | 84 | (1,252.00) | (1,154.98) |
| 2 | (1,000) | (224) | 56 | (1,168.00) | (994.00) |
| 3 | (1,000) | (112) | 28 | (1,084) | (851.02) |
| Total | (3,000.00) | ||||
[latex](.112)(1-.25)=.084[/latex] This is the after-tax interest rate.
Note: The present value of loan payments will always equal the value of the asset as long as the loan is not subsidized which means the loan rate is less than the current market rate.
[latex]^{2}(3,000)(.25)(\frac{{.4}}{{.4+.084}})(\frac{{2+.084}}{{2(1+.084)}})[/latex]
3
| Year | Lease Payment | Tax Savings (.25) | After-tax Cost of Leasing | Present Value (8.40%) |
| 0 | (1,200.00) | 0.00 | (1,200.00) | (1,200.00) |
| 1 | (1,200.00) | 300.00 | (900.00) | (830.26) |
| 2 | (1,200.00) | 300.00 | (900.00) | (765.92) |
| 3 | 300.00 | 300.00 | 235.52 | |
| Total | (2,560.66) | |||
2.
The after-tax cost of debt was used as the discount rate and not the WACC because the lease is a substitute for the loan. It represents the riskiness of those future cash flows.
H. Lease or Buy at Shaw
1.
Lease? No
| Investment | 100,000.00 |
| Lost CCA tax shield1 | (18,686.50) |
| Present value of lease payments2 | (85,508.96) |
| Present value of lost disposal value3 | (6,274.12) |
| Present value of CCA tax shield on lost disposal value4 | 1,868.65 |
| Total | (8,600.93) |
The investment value was not calculated as in the problem above (G) because that problem demonstrated that the present value of loan payments will always equal the value of the asset as long as the loan is not subsidized, that is, that the loan rate is not less than the current market rate.
[latex]^{1}(100,000)(.25)(\frac{{.20}}{{.20+.06}})(\frac{{2+.06}}{{2(1+.06)}})[/latex]
[latex](.08)(1-.25)=.06[/latex]
2
| Year | Lease Payments | Tax Shield (.25) | After-tax Cost of Leasing | Present Value (6.00%) |
| 0 | (17,000.00) | (17,000.00) | (17,000.00) | |
| 1 | (17,000.00) | 4,250.00 | (12,750.00) | (12,028.30) |
| 2 | (17,000.00) | 4,250.00 | (12,750.00) | (11,347.45) |
| 3 | (17,000.00) | 4,250.00 | (12,750.00) | (10,705.15) |
| 4 | (17,000.00) | 4,250.00 | (12,750.00) | (10,099.19) |
| 5 | (17,000.00) | 4,250.00 | (12,750.00) | (9,527.54) |
| 6 | (17,000.00) | 4,250.00 | (12,750.00) | (8,988.25) |
| 7 | (17,000.00) | 4,250.00 | (12,570.00) | (8,479.48) |
| 8 | 4,250.00 | 4,250.00 | 2,666.50 | |
| Total | (85,508.86) | |||
[latex]^{3}\frac{{10,000}}{{(1+.06)^{8}}}[/latex]
[latex]^{4}\frac{{(10,000)(.25)(\frac{{.20}}{{.20+.06}})(\frac{{2+.06}}{{2(1+.06)}})}}{{(1+.06)^{8}}}[/latex]
I. Lease or Buy at Anzio
1.
Lease? No.
| Investment | 2,700,000.00 |
| Lost CCA tax shield on the building1 | (220,840.48) |
| Present value of lease payments2 | (2,580,732.27) |
| Present value of lost disposal value of the building3 | (31,180.47) |
| Present value of lost CCA tax shield disposal on the building4 | 11,042.02 |
| Present value of lost disposal value of the land5 | (300,112.05) |
| Total | (421,823.25) |
[latex]^{1}(2,000,000)(.25)(\frac{{.05}}{{.05+.06}})(\frac{{2+.06}}{{2(1+.06)}})[/latex]
[latex](.08)(1-.25)[/latex]
Note: unlike some of the earlier problems, this is an ordinary annuity because the payment is due at the end of the year.
[latex]^{2}(300,000)(1-.25)(\frac{{1-(1+.06)^{-20}}}{{.06}})[/latex]
[latex]^{3}\frac{{100,000}}{{(1+.06)^{20}}}[/latex]
[latex]^{4}\frac{{(100,000)(.25)(\frac{{.05}}{{.05+.06}})(\frac{{2+.06}}{{2(1+.06)}})}}{{(1+.06)^{20}}}[/latex]
[latex]^{5}\frac{{(1,000,000-(1,000,000-700,000)(.50)(.25))}}{{(1+.06)^{20}}}[/latex]
This is the present value of the estimated value of the land at the end of the lease less the tax on the profit the company would realize if it sold the land at that time. It bought it for 700,000, sold it for 1,000,000, realizing 300,000 profit which is a long term gain (taxed at 1/2 the normal rate) and the tax rate is 25%.
J. Lease or Buy at Olesen
1.
Lease? No
| Investment | 40,000.00 |
| Lost CCA tax shield1 | <8,038.92> |
| Present value of lease payments2 | <25,854.98> |
| Present value of lost residual3 | <7,854.05> |
| Present value of lost CCA tax shield on residual4 | 1,578.45 |
| Total | <169.50> |
[latex]^{1}(40,000)(.25)(\frac{{.30}}{{.30+.062}})(\frac{{2+.062}}{{2(1+.062)}})[/latex]
Note that the interest rate on the loan is a monthly APR while the lease payments are annual. The interest rate used must always match the number of compounding periods in a year, so we must first find the Effective Annual Rate.
Or 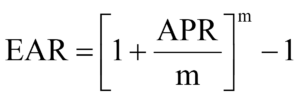
[latex]{\left( {1 + \frac{{.08}}{{12}}} \right)^{12}} - 1[/latex] or 0.0829995 or EAR ≈ 8.3%.
We then find the after-tax rate 0.083 (1-.25)=0.062
[latex]^{2}(10,000)(1-.25)(\frac{{1-(1+.062)^{-4}}}{{.062}})[/latex]
[latex]^{3}\frac{{10,000}}{{(1+.062)^{4}}}[/latex]
[latex]^{4}\frac{{(10,000)(.25)(\frac{{.30}}{{.30+.062}})(\frac{{2+.062}}{{2(1+.062)}})}}{{(1+.062)^{4}}}[/latex]
K. Lease or Buy at Halo Manufacturing
Note: Assume this is exempt specified leasing property under the Income Tax Act.
1.
Lease? No.
| Machine | 80,000.00 |
| Lost CCA tax shield on the machine1 | <16,077.85> |
| Present value of lease payments2 | <56,369.91> |
| Present value of lost disposal value of the machine3 | <14,787.58> |
| Present value of lost CCA tax shield disposal on the machine4 | 2,971.91 |
| Total | (4,263.43) |
[latex]^{1}(80,000)(.25)(\frac{{.30}}{{.30+.06}})(\frac{{2+.06}}{{2(1+.06)}})[/latex]
Note that the interest rate on the loan is a monthly APR while the lease payments are annual. The interest rate used must always match the number of compounding periods in a year, so we must first find the Effective Annual Rate.
Or ![]()
[latex]{\left( {1 + \frac{{.08}}{{12}}} \right)^{12}} - 1[/latex] or 0.0829995 or EAR ≈ 8.3%.
We then find the after-tax rate 0.083 (1-.25)=0.062
[latex]^{2}(16,900)(1-.25)(\frac{{1-(1+.062)^{-4}}}{{.062}})[/latex]
[latex](16,900)(1-.25)+(16,900)(1-.25)(\frac{{1-(1+.062)^{-4}}}{{.062}})[/latex]
Note: This is an annuity due, payable at the beginning of the year.
[latex]^{3}\frac{{20,000}}{{(1+.062)^{5}}}[/latex]
[latex]^{4}\frac{{(20,000)(.25)(\frac{{.30}}{{.30+.062}})(\frac{{2+.062}}{{2(1+.062)}})}}{{(1+.062)^{5}}}[/latex]
L. Specified Leasing Property
1.
High Country would declare the lease payment as income and deduct against it the lower of: 1) CCA or 2) the principal a lessor receives if a lease is treated as a loan equal to the fair value of the leased asset. The net of these two amounts is equivalent to the interest portion of the loan payment. This is what the lessor would recognize if they treated the lease as a loan, which is the intention of the government. The interest rate used to calculate the principal is the prescribed rate published by the Bank of Canada.
| Lease payment | 48,750 |
| Minus CCA calculated as the lesser of: | |
| Actual CCA: (200,000) (.40) (.50) = 40,000 | |
| Principal portion of loan: 48,750 – (200,000)(.06) = 36,750 | (36,750) |
| Net amount | 12,000 |
2.
Normally Langston deducts the entire lease payment as an expense, but it can elect to instead deduct the interest portion of the payment and CCA.
| Lease Payment | 48,750 |
| CCA: (200,000) (.40) (.50) = 40,000 | 40,000 |
| Interest: (200,000) (.06) = 12,000 | 12,000 |
| Total | 52,000 |
Langston would have higher deductions by electing to treat the leased asset as if they bought it with a loan. The difference will be greater next year when the Half-Year Rule no longer applies. Lessees will make this election for assets that are written off quickly and have a high CCA rate.
M. Bond Refunding at Acme
1.
Yes, because the Net Present Value calculated below of 174,342.36 is positive.
| Call premium1 | (150,000.00) |
| Issuance costs new issue2 | (82,191.49) |
| Issuance costs old issue3 | 7,300.00 |
| Overlapping interest4 | (37,762.50) |
| Cost savings of lower interest5 | 436,996.35 |
| Total | 174,342.36 |
[latex]\begin{array}{lll}^{1}(5,000,000)(.04)=200,000\\(200,000)(1-.25)=150,000\end{array}[/latex]
To recall the old bond, Acme must pay a premium of 4% of the face or par value of the bond issue or $200,000, but this is a tax-deductible expense, so the after-tax call premium is 150,000.
[latex]\begin{array}{rcl}^{2}105,000-^{1}22,808.51&=&82,191.49\\^{1}(\frac{{105,000}}{{5}})&=&21,000\\(21,000)(.25)&=&5,250\\5,250(\frac{{1-(1+.04875)^{-5}}}{{.04875}})&=&22,808.51\end{array}[/latex]
Total issuance costs on the new bond are 90,000+15,000=105,000.
This cost is amortized over 5 years which provides a tax deduction each year. The depreciation each year is 21,000 which provides a tax deduction of 5,250 per year for 5 years. The present value of these tax deductions is 22,808.51. The 5,250 occurs each year for 5 years and must be discounted back to the present. This is an annuity problem where the 5,250 is the PMT, N=5, and i/y or r = 4.875 using a financial calculator or 0.04875 using the formula given above. This rate is the after-tax interest rate on the new bonds – see question 2 and its answer below.
[latex]\begin{array}{lll}^{3}\frac{{(60,000+13,000)}}{{5}}&=&14,600\\(14,600)(2)(.25)&=&7,300\end{array}[/latex]
The old bonds had total issuance costs of 73,000 which was depreciated over 5 years for an annual depreciation of 14,600. There are 2 years of depreciation left, which can immediately be written off. This is a tax-deductible expense and so provides an immediate tax deduction 7,300.
[latex]\begin{array}{rcl}^{4}(.08)(\frac{{2}}{{12}})(5,000,000)(1-.25)&=&50,000.00\end{array}[/latex]
You issue the new bonds 2 months before you payoff the old bonds. You must pay interest on the old bonds during this time. That is (.08) (2/12) (5,000,000), but as this is a tax-deductible expense, your after-tax interest cost is only 50,000.00.
[latex]\begin{array}((.02)(\frac{{2}}{{12}})(4,895,000)(1-.25)&=&12,237.50\end{array}[/latex]
Since you issued the new bonds, but do not pay off the old bonds for 2 months, you can invest the proceeds of the bond sale temporarily at 2.0%. However, you did have to pay 105,000 in total issuance costs, so you only have 4,895,000 to invest temporarily. In addition, this income is taxable, so the after-tax income is 12,237.50
[latex]\begin{array}\\50,000.00-12,237.50&=&37,762.50\end{array}[/latex]
This is the net after-tax interest costs on the bonds during the 2-month overlap period.
5,000,000-105,000
5 (5,000,000) (.08) (1 – .25) = 300,000
After-tax interest cost on the old bonds per year.
[latex]\begin{array}\\(5,000,000)(.065)(1-.25)&=&243,750\end{array}[/latex]
After-tax cost interest cost on the new bonds per year.
[latex]\begin{array}\\300,000-243,750&=&56,250\end{array}[/latex]
The company saves 56,250 per year after taxes over the 10-year life of the bond. We need to find the Present Value of this annual savings, so the 56,250 is the annuity payment, the rate is 4.875 percent, and the annuity lasts 10 years.
[latex]\begin{array}\\56,250(\frac{{1-(1+.04875)^{-10}}}{{.04875}})&=&436,996.35\end{array}[/latex]
2.
[latex](.065)(1-.25)=.04875[/latex]
N. Bond Refunding at Hansen Brothers
1.
Yes.
| Call premium1 | (450,000.00) |
| Issuance costs2 | (319,628.06) |
| Overlapping interest3 | (42,828.12) |
| Cost savings of lower interest4 | 1,076,139.14 |
| Total | 263,682.96 |
[latex]\begin{array}{lll}^{1}(15,000,000)(.04)&=&600,000\\(600,000)(1-.25)&=&450,000\end{array}[/latex]
[latex]\begin{array}{rcl}^{2}410,000.00-^{1}90.371.94&=&319,628.06\\^{1}(\frac{{410,000}}{{5}})&=&82,000\\(82,000)(.25)&=&20,500\\(0.58)(1-.25)&=&.0435\\20,500(\frac{{1-(1+.0435)^{-5}}}{{.0435}})&=&90,371.94\end{array}[/latex]
[latex]\begin{array}{rcl}^{3}(.07)(\frac{{1}}{{12}})(15,000,000)(1-.25)&=&65,625.00\\(.025)(\frac{{1}}{{12}})(^{1}14,590,000)(1-.25)&=&22,796.88\\65,625.00-22,796.88&=&42,828.12\\^{1}15,000,000-410,000\end{array}[/latex]
[latex]\begin{array}{rcl}^{4}(15,000,000)(.070)(1-.25)&=&787,500\\(15,000,000)(.058)(1-.25)&=&652,500\\787,500-652,500&=&135,000\\135,000(\frac{{1-(1+0435)^{-10}}}{{.0435}})&=&1,076,139.14\end{array}[/latex]
2.
To eliminate restrictive covenants contained in the previous loan agreement.
3.
Hanson Brothers will have to buy back the bonds at an amount that approximates their current market value. Similar bonds are currently yielding 5.8 % and Hanson Brothers will have to buy back the bonds at value computed using a discount rate of 5.7 % (Canada Bond rate of 4.5 % plus premium of 1.2 %). This value will fairly compensates the bondholder for the higher interest rates they are being forced to give up and eliminates any interest savings the borrower can realize. Remember that when market interests fall, bond prices rise because investors continue to receive the higher coupon rate stipulated in the bond indenture.
O. Preferred Share Refunding at Spencer
1.
Yes.
| Call premium1 | <100,000.00> |
| Issuance costs2 | <127,198.42> |
| Cost savings of lower interest3 | 857,142.86 |
| Total | 629,944.44 |
[latex]^{1}(2,000,000)(.05)=100,000[/latex]
Note: Call premiums on equity are not tax deductible.
[latex]\begin{array}{rcl}^{2}160,000-^{1}32,801.58&=&127,198.42\\^{1}(\frac{{160,000}}{{5}})&=&32,000\\(32,000)(.25)&=&8,000\\8,000(\frac{{1-(1+.07)^{-5}}}{{.07}})&=&32,801.58\\\frac{{5}}{{71.43}}&=&.07\end{array}[/latex]
Notes: Discount rate for preferred shares financing is equal to the dividend divided by the market value of a preferred share. Dividends are not tax deductible so do not include the tax effect.
[latex]\begin{array}{rcl}^{3}(2,000,000)(.10)&=&200,000\\(2,000,000)(.07)&=&140,000\\200,000-140,000&=&60,000\\\frac{{60,000}}{{.07}}&=&857,142.86\end{array}[/latex]
P. Classifying Assets and Liabilities
- Classified as equity because the preferred share dividends can be delayed indefinitely and there are no required sinking fund payments.
- Classified as equity because the preferred share dividends can be delayed indefinitely and there are no required sinking fund payments. The preferred share dividends are cumulative which means the common shareholders cannot receive a dividend until all the dividends in arrears are paid, but if the company is in financial distress these dividends can still be delay indefinitely.
- Classified as debt because the preferred share dividends must be paid or the company can be forced into bankruptcy.
- Classified as debt because the preferred shares have required sinking fund payments. If the sinking fund payments only had to be paid on a best efforts basis, then these payments would not be required so the preferred share would be classified as equity.
- Classified as debt because the bondholder can force the company to buy back the bonds. The company has no control over this decision.
- Classified as debt because the dividend grows over time and eventually the company will have no choice but to buy back these shares if it is to survive.
- Classified as debt since the interest must be paid even though the bonds have an unlimited life.
- Classified as equity since interest payments are not guaranteed and principal payments are subordinate to all other bondholders.
- Classified as equity since the interest and principal payments can be settled by issuing common equity which do not have any required payments.
Q. Rights Offering at Quaker
1.
Subscription Price
[latex](.75)(8)=6[/latex]
Number of New Common Shares
[latex]\frac{{12,000,000}}{{6}}=2,000,000[/latex]
Number of Rights to Buy One Common Share
[latex]\frac{{10,000,000}}{{2,000,000}}=5[/latex]
2.
Yes, Dunne retains the same ownership percentage by exercising her rights.
Number of Shares Purchased
[latex]\frac{{((10,000,000)(.4))}}{{5}}=800,000[/latex]
Percentage Ownership
[latex]=\frac{{(4,000,000+800,000)}}{{(10,000,000+2,000,000)}}=.40{\text{ or }}40{\text{%}}[/latex]
No, the value of Dunne’s investment is not diluted by the drop in common share price due to the low subscription price. Her shares continue to be worth 40% of the value of the company after the rights issue. Why? The value of the company increased by CAD12,000,000 when the new shares were sold. It is arbitrary whether this was raised by selling 2,000,000 shares at CAD6, 1,500,000 at CAD8 or any other combination. The overall value of the firm will remain the same as will the value of a shareholder’s investment in relation to the value of the firm.
New Company Common Share Price
[latex]=\frac{{(10,000,000)(8)+(2,000,000)(6)}}{{(10,000,000+2,000,000)}}=7.6667[/latex]
Value of Dunne’s 40% Share
[latex](4,000,000+800,000)(7.6667)=36,800,160[/latex]
Value of Company
[latex](10,000,000)(8)+(2,000,000)(6)=92,000,000[/latex]
or
[latex](10,000,000+2,000,000)(7.6667)=92,000,400{\text{(rounding error)}}[/latex]
Value of Dunne’s 40% Share in Relation to Company
[latex]=\frac{{36,800,160}}{{92,000,000}}=.40[/latex]
R. Appropriate Forms of Debt and Equity Financing
- A syndicated loan allows a number of credit unions or other institutional investors to pool their capital and share risk.
- A bridge loan can provide financing until the proceeds of the private bond placement are received.
- Project financing that establishes a special purpose vehicle (SPV) and employs non-recourse financing to reduce risk can be employed.
- The food critic can use their popularity to raise crowdfunding from local fans. Contributors may receive debt or equity securities in the company or a reward such as a meal voucher.
- Mezzanine debt financing that is subordinate to the existing debt can provide the funds required. It will likely be convertible into common shares if the company does not make its principal and interest payments, so losing control is still a potential issue.
- Securitization can be used to sell the leases when they are originated so financing is not required. The leasing company can maintain a relationship with its customers and continue to earn fee income servicing the contracts.
- A bridge loan can provide funding for payroll and other operating expenses until the third round of venture capital financing is received.
- A joint venture can be formed with another company(s) that has sufficient capital to produce and market the product internationally.
- A sale leaseback agreement can be negotiated to finance the tractor trailers.
- Project financing can be used by the government development group to limit their risk and access external financing and management expertise.
- The entrepreneur can use self funding for the equity component of the investment and negotiate a bank loan for the remainder. A loan is easier to secure if the client is a member of a successful franchise.
- The entrepreneur can apply to an incubator or accelerator program to help them raise angel or venture capital.
- The controlling shareholders can limit the mature company’s growth to a level that is supportable by its retained earnings to avoid losing control and high issuance costs.
- Business Development Bank of Canada can provide the flexible loan terms and collateral requirements desired because of their non-profit status and goal of promoting employment and economic development by aiding small businesses.
- Export Development Corporation can provide the financing needed to accept this export order because of their non-profit status and goal of promoting employment and economic development by promoting exports.
- A bridge loan can provide financing to buyout the existing partner until the new partner invests in the firm.
- Private equity placement using an Offering Memorandum or selling shares to Accredited Investors, friends, family, business associates, employees, directors, officers, or consultants can be used to raise funds.
- Corporate venture capital can be sought as the firm sponsoring the fund will probably buyout the company if it is successful. This provides the entrepreneur with a simple exit strategy.
- Loan prepayment privileges, callable bonds with limited call or refund protection, or floating interest rates will protect the company from falling interest rates.
- An ESOP will promote labour-management harmony by increasing employee ownership. ESOPs and DRIPs will help establish a core group of investors that will likely remain loyal during a take-over attempt.
- Crowdfunding can be used by the band to raise funds to produce the album and cover initial tour costs. Contributors can be given a free album and/or concert ticket(s).
- Preferred shares can give the flexibility to delay dividend payments during an economic downturn without triggering bankruptcy.
- Equity can be raised using non-voting, restricted, or multi-voting shares.
- The company can remain private and use private placements with one or more institutional investors to raise the needed capital.
- Public debt and equity placements will probably result in the lowest interest rate due to the liquidity of the public markets. Flexible bond or debenture agreements can be negotiated if the company has a strong credit rating.
- A personal or limited or full third-party guarantee can be provided to compensate for low-quality collateral.

