Module 7 Answer Key
7.10 Exercises
A. Suitability of Income Approach (DDM) at Quesnel
1.
Little Fort – Yes
From 2009 to 2016, Little Fort’s EPS has grown at a compounded annual growth rate of 8.0% while DPS have grown at 9.0%. The dividend payment ratio has been tightly ranged from 0.49 to 0.53. Little Fort is a dividend paying company that has shown a consistent relationship between earnings and dividends.
Clearwater – No
From 2009 to 2016, Clearwater’s EPS has grown slightly and has been erratic. Dividends have remained constant. The dividend payment ratio ranged from 0.35 to 1.13. Clearwater is a dividend paying company but it has not shown a consistent relationship between earnings and dividends. Its policy is simply to maintain a constant dividend so not to disappoint shareholders.
B. Income Approach (DDM) at Rebel
1.
V0 = [latex]\frac{{\left( {10} \right){{\left( {1 + .07} \right)}^1}}}{{{{\left( {1 + .1555} \right)}^1}}}[/latex] + [latex]\frac{{\left( {10} \right){{\left( {1 + .07} \right)}^2}}}{{{{\left( {1 + .1555} \right)}^2}}}[/latex] + [latex]\frac{{\left( {10} \right){{\left( {1 + .07} \right)}^3}}}{{{{\left( {1 + .1555} \right)}^3}}}[/latex] + [latex]\frac{{\frac{{\left( {10} \right){{\left( {1 + .07} \right)}^3}\left( {1 + .03} \right)}}{{\left( {.1555 - .03} \right)}}}}{{{{\left( {1 + .1555} \right)}^3}}}[/latex] = CAD 90.94
kc = .04 + 2.1 (.095 – .04) = .1555 or 15.55%
Yes, the shares appear to be currently overvalued so the company should issue new shares now before the market corrects itself.
2.
Best Case
V0 = [latex]\frac{{\left( {10} \right){{\left( {1 + .09} \right)}^1}}}{{{{\left( {1 + .1555} \right)}^1}}}[/latex] + [latex]\frac{{\left( {10} \right){{\left( {1 + .09} \right)}^2}}}{{{{\left( {1 + .1555} \right)}^2}}}[/latex] + [latex]\frac{{\left( {10} \right){{\left( {1 + .09} \right)}^3}}}{{{{\left( {1 + .1555} \right)}^3}}}[/latex] + [latex]\frac{{\left( {10} \right){{\left( {1 + .09} \right)}^4}}}{{{{\left( {1 + .1555} \right)}^4}}}[/latex] + [latex]\frac{{\frac{{\left( {10} \right){{\left( {1 + .09} \right)}^4}\left( {1 + .04} \right)}}{{\left( {.1555 - .04} \right)}}}}{{{{\left( {1 + .1555} \right)}^4}}}[/latex] = CAD 105.94
Worst Case
V0 = [latex]\frac{{\left( {10} \right){{\left( {1 + .05} \right)}^1}}}{{{{\left( {1 + .1555} \right)}^1}}}[/latex] + [latex]\frac{{\left( {10} \right){{\left( {1 + .05} \right)}^2}}}{{{{\left( {1 + .1555} \right)}^2}}}[/latex] + [latex]\frac{{\frac{{\left( {10} \right){{\left( {1 + .05} \right)}^2}\left( {1 + .02} \right)}}{{\left( {.1555 - .02} \right)}}}}{{{{\left( {1 + .1555} \right)}^2}}}[/latex] = CAD 79.50
No, after using a best and worst-case analysis, the shares still appear to be overvalued so the company should issue new shares before the market corrects itself.
C. Income Approach (DDM) With No Growth at Roanoke
1.
kp = 9.22%
Vo = [latex]\frac{{\left( {.035} \right)\;\left( {100} \right)}}{{.0922\;}}[/latex] = CAD 37.96
D. Income Approach (DDM) With Negative Growth at Klondike
1.
kc = .04 + 1.3 (.055) = .1115 or 11.15%
[latex]{V_0} = \frac{{{D_0}\left( {1 + g} \right)}}{{{k_e} - g}} = \frac{{2.50\left( {1 + \left( { - .05} \right)} \right)}}{{.1115 - \left( { - \;.05} \right)}}[/latex] = CAD 14.71
E. Estimating Historical Growth Rates
1.
Arithmetic Mean Historical Growth Rate
(156.52% + 8.33% + 23.08% + (-9.38%) + 20.69% + (-27.62%) + 18.42% + 1.11% + 39.56% + (-11.02%) + 12.39%) / 11 = 12.01%
1(.72 – .46) / .46 = .5652 or 56.52% Note: growth is the percentage change from one year to the next: (ending value-beginning value)/beginning value.
Geometric Mean Historical Growth Rate
(.46) (1 + i)11 = 1.27
i = .0967 or 9.67%
Geometric mean can be solved in Excel or using a financial calculator. Using a financial calculator, enter the beginning value as the PV, the ending value as the FV (remember that either the PV or FV must be entered as a negative number to distinguish the direction of cash flow), and N is the number of years. Solve for the rate, i/y.
Geometric mean should be used because it gives an accurate long-term measure of the growth rate and is not affected by the moving base like the arithmetic mean. The difference between the arithmetic and geometric mean growth rate increases as growth rates become more volatile.
2.
Regression Smoothing (see the Excel file for 2 methods of regression smoothing.)
y = .5692 + .0545 (x)
Year 1 .5692 + .0545 (1) = .6237
Year 12 .5692 + .0545 (12) = 1.2232
(.6237) (1 + i) 11 = 1.2232
i = .0631 or 6.31%
Geometric mean growth rate with regression smoothing addresses the problem of the first and last value being outliers and thus distorting the geometric mean. EPS of CAD .46 in 2005 appears to have been an outlier and this approach helps to correct for this resulting in a lower growth rate. This approach also deals better with negative EPS figures. With geometric mean it becomes a problem when the first or last values are negative. For arithmetic mean, percentage changes are not meaningful when the base is negative.
F. Income Approach (DDM) at Amsterdam
This problem, like the ones before it, all follow the same pattern. V0 = D1/(1+k)^1 + D2/(1+k)^2 + D3/(1+k)^3 + … Dn/(1+k)^n + [Dn+1/(k-g)]/(1+k)^n
(4.50)(.25)(1+.290)^1 is D1 and (4.50)(.75)(1+.290)^3 (1+.032) is Dn+1 or D4 in this particular problem.
We don’t know the dividend, but we do know the earnings per share (or Net Income per share). Earnings or net income must either be retained (to become retained earnings) or given to shareholders as dividends. The payout ratio (POR) is the % of NI or EPS given to shareholders as dividends, so EPS*POR=dividend. So EPS0*POR = D0 and EPS0*POR*(1+g) = D1
where g is growth in the first year.
(4.50)(1+.290)^3 is EPS3 and (4.50)(1+.290)^3 (1+.032) is EPS4. Note that the POR changed from 25% to 75% in year 4, so 75% of EPS4 is D4.
As in prior problems, the growth rate changed the last year, from 29% to 3.2%. A final change in this problem is that the required rate of return also changes from 11.1% to 10%. You can see both of these changes in the calculation of the terminal value:
[latex]\frac{{\left( {4.50)(.75} \right){{\left( {1 + .290} \right)}^3}\left( {1 + .032} \right)}}{{\left( {.100 - .032} \right)}}[/latex] which uses the growth rate in the terminal year (3.2%) and the required return K of 10%. Remember the terminal value is the value the year before the dividend growth goes constant. The dividend growth goes constant in year 4, so the terminal value is as of year 3, and so like the dividend received in year 3, it must be discounted back to the present using the required return which was required in year 3 or 11.1%. This is why the terminal value is divided by (1+.111)^3.
1.
V0 = [latex]\frac{{{D_1}}}{{{{\left( {1 + {k_e}} \right)}^1}}} + \frac{{{D_2}}}{{{{\left( {1 + {k_e}} \right)}^2}}} + \frac{{{D_3}}}{{{{\left( {1 + {k_e}} \right)}^3}}} + \frac{{terminal\;value}}{{{{\left( {1 + {k_e}} \right)}^3}}}[/latex]
V0 = [latex]\frac{{\left( {4.50)(.25} \right){{\left( {1 + .290} \right)}^1}}}{{{{\left( {1 + .111} \right)}^1}}}[/latex] + [latex]\frac{{\left( {4.50} \right)\left( {.25} \right){{\left( {1 + .290} \right)}^2}}}{{{{\left( {1 + .111} \right)}^2}}}[/latex] + [latex]\frac{{\left( {4.50)(.25} \right){{\left( {1 + .290} \right)}^3}}}{{{{\left( {1 + .111} \right)}^3}}}[/latex] +
[latex]\frac{{\frac{{\left( {4.50)(.75} \right){{\left( {1 + .290} \right)}^3}\left( {1 + .032} \right)}}{{\left( {.100 - .032} \right)}}}}{{{{\left( {1 + .111} \right)}^3}}}[/latex] = CAD 84.76
Terminal value
High-Growth Stage
Ke = .045 + 1.2 (.055) = .111
ROE = (.15 / (1 – .50) = .300
g = (.300 / (1 – .25) / (1 – (.300) (1 – .25)) = .290
Stable-Growth Stage
Ke = .045 + 1.0 (.055) = .100
ROE = .05 / (1 – .60) = .125
g = (.125) (1 – .75) / (1 – (.125) (1 – .75)) = .032
2. Terminal value accounts for 95% (80.18 ÷ 84.76) of Amsterdam’s intrinsic value. Small errors in estimating the inputs used to calculate terminal value will have a significant effect on the valuation of the company.
G. Income Approach (DDM) at Samantha
|
Year 1 |
Year 2 |
Year 3 |
Year 4 |
Year 5 |
|
| ROA |
0.1800 |
0.1800 |
0.1500 |
0.1200 |
0.0900 |
| Debt ratio |
0.2000 |
0.2000 |
0.2667 |
0.3333 |
0.4000 |
| ROE |
0.2250 |
0.2250 |
0.2045 |
0.1800 |
0.1500 |
| Payout ratio |
0.2500 |
0.2500 |
0.4167 |
0.5833 |
0.7500 |
| Sustainable growth |
0.2030 |
0.2030 |
0.1355 |
0.0811 |
0.0390 |
| Beta |
1.3600 |
1.3600 |
1.2400 |
1.1200 |
1.0000 |
| Risk-free rate |
0.0400 |
0.0400 |
0.0400 |
0.0400 |
0.0400 |
| Market risk premium |
0.0500 |
0.0500 |
0.0500 |
0.0500 |
0.0500 |
| Cost of equity |
0.1080 |
0.1080 |
0.1020 |
0.0960 |
0.0900 |
V0 = [latex]\frac{{7.70}}{{1.1080}}[/latex] + [latex]\frac{{9.26}}{{1.2277}}[/latex] + [latex]\frac{{10.51}}{{1.3529}}[/latex] + [latex]\frac{{11.36}}{{1.4828}}[/latex] + [latex]\frac{{\frac{{11.80}}{{\left( {.09\; - .0390} \right)}}}}{{1.4828}}[/latex] = CAD 185.84
Dividend Growth
Year 1 (6.40) (1 + .2030) = 7.70
Year 2 (7.48) (1 + .2030) = 9.26
Year 3 (8.74) (1 + .1355) = 10.51
Year 4 (9.78) (1 + .0811) = 11.36
Year 5 (10.51) (1 + .0790) = 11.80
Discount Rates
Year 1 (1 + .108) = 1.1080
Year 2 (1.1080) (1 + .1080) = 1.2277
Year 3 (1.2277 (1 + .1020) = 1.3529
Year 4 (1.3529) (1 + .0960) = 1.4828
H. Income Approach (DDM) at ABC
-
Year 1
Year 2
Year 3
Year 4
Year 5
ROA 0.1900 0.1900 0.1400 0.0900 0.0400 Debt ratio 0.2000 0.200 0.3500 0.5000 0.6500 ROE 0.2375 .2375 .2154 .1800 0.1143 Payout ratio 0.3500 0.3500 0.4300 0.5100 0.5900 Sustainable growth 0.1826 0.1826 0.1400 0.0967 0.0492 Beta 1.0500 1.0500 1.0000 0.9500 0.9000 Risk-free rate 0.0500 .0500 0.0500 .0500 .0500 Market risk premium 0.0450 0.0450 0.0450 0.0450 .0450 Cost of equity 0.0973 .0973 .0950 .0928 .0905 V0 = [latex]\frac{{4.16}}{{1.0973}}[/latex] + [latex]\frac{{4.92}}{{1.2040}}[/latex] + [latex]\frac{{5.61}}{{1.3183}}[/latex] + [latex]\frac{{6.15}}{{1.4406}}[/latex] + [latex]\frac{{\frac{{6.45}}{{\left( {.0905\; - .0492} \right)}}}}{{1.4406}}[/latex] = CAD 124.71
Dividend Growth
Year 1 (3.52) (1 + .1826) = 4.16
Year 2 (4.66) (1 + .1826) = 4.92
Year 3 (4.92) (1 + .1400) = 5.61
Year 4 (5.61) (1 + .0967) = 6.15
Year 5 (6.15) (1 + .0492) = 6.45
- Discount Rates
- Year 1 (1 + .0973) = 1.0973
- Year 2 (1.0973) (1 + .0973) = 1.2040
- Year 3 (1.2041) (1 + .0950) = 1.3183
- Year 4 (1.3185) (1 + .0928) = 1.4406
I. Implied Growth Rate of Dividends
1.
gd = [latex]\frac{{\left( {{{\rm{V}}_0}} \right)\left( {{{\rm{k}}_{\rm{c}}}} \right) - {\rm{\;}}{{\rm{D}}_0}}}{{{{\rm{V}}_0} + {\rm{\;}}{{\rm{D}}_0}}}[/latex]
kc = .04 + 1.2 (.055) = .1060
gd = [latex]\frac{{\left( {45} \right)\;\left( {.1060} \right)\; - \;1.35}}{{45 + \;1.35}}[/latex] = .0738 or 7.38%
The implied gd of this mature company is 7.38% at a current market price of CAD 45, which is unreasonable compared to the nominal long-term growth rate of the economy of 3.75% (2% + 1.75%) – it will eventually become the economy. The current price is based on this higher growth rate and is too high. A more reasonable share price estimate is:
Vo = [latex]\frac{{\left( {1.35} \right)\left( {1 + \;.0375} \right)}}{{.1060\; - \;.0375}}[/latex] = CAD 20.45
J. Income Approach (FCFE) at Shelton
1.
kc = rf+β*MRP =.04 + 1.25 (.05) = .1025
V0 = [latex]\frac{{{D_0}\left( {1 + g} \right)}}{{{k_e} - g}} = \frac{{\left( {1.65} \right)\left( {1 + \;.03} \right)}}{{.1025 - \;.03}}[/latex] = CAD 23.44 per share
2. Note that enterprise level values must be divided by the number of shares to get per share value use here.
New Debt is the debt ratio times the sum of Capital Expenditures and the increase in Working Capital less depreciation.
We will estimate FCFE on a per share basis. Note that Net Income is then EPS.
FCFE = Net income + Non-cash charges – Net capital expenditures – Change in working capital + New debt – Principal payments
FCFE = 3.15 + [latex](\frac{{\left( {305} \right)}}{{155}}) – (\frac{{\left( {465} \right)}}{{155}})\;– (\frac{{\left( {25} \right)}}{{155}}) – (\frac{{\left( {465 - 305 + 25} \right)\left( {\;.2} \right)}}{{155}})[/latex] = CAD 2.20 per share
V0 = [latex]\frac{{FCF{E_0}\left( {1 + g} \right)}}{{{k_e} - g}} = \frac{{\left( {2.20} \right)\left( {1 + \;.03} \right)}}{{.1025 - \;.03}}[/latex] = CAD 31.26 per share
3.
- Dividend growth normally lags growth in earnings and FCFE
- Cash is being retained instead of being paid out as dividends – why?
- Investments in unprofitable projects
- Keeping current dividend low to ensure that it can always be paid
- Used to reduce debt creating a sub-optimal debt ratio
- Lower tax rate on capital gains encouraging higher earnings retention
K. Income Approach (FCFE) at Global
-
2010
2011
2012
Net income 9,000
9,450
9,923
Add: Depreciation 9,000
9,450
9,922
Minus: Capital expenditures 11,000
11,550
12,127
Minus: Increase in NWC 1,000
1,050
1,102
Add: Increase in long-term debt 2,000
2,100
2,205
FCFE
8,000
8,400
8,821
kc = .04 + 1.30 (.05) = .105
V0 = [latex]\frac{{8,000}}{{{{\left( {1 + \;.105} \right)}^1}}}[/latex] + [latex]\frac{{8,400}}{{{{\left( {1 + \;.105} \right)}^2}}}[/latex] + [latex]\frac{{8,821}}{{{{\left( {1 + \;.105} \right)}^3}}}[/latex] + [latex]\frac{{\frac{{\left( {8,821} \right)\left( {1 + \;.03} \right)}}{{\left( {.105\; - .03} \right)}}}}{{{{\left( {1 + \;.105} \right)}^3}}}[/latex] = CAD 110,443
L. Income Approach (FCFE) at Ricco
-
Year 1
Year 2
Year 3
EPS 4.311
5.801
5.994
Minus: (CE – D) (1 – DR) .522
.702
–
Minus: Increase NWC (1 – DR) .573
.773
.075
FCFE
3.22
4.33
5.92
1 .20 / (1 – .30) = .2857
(.2857) (.9) / (1 – (.2857) (.9)) = .3461
(3.20) (1 + .3461) = 4.31
(4.31) (1 + .3461) = 5.80
2 (1.25 – .70) (1 + .3461) (1 – .30) = .52
(.52) (1 + .3461) = .70
3 ((15.70) (1 + .3461) – 15.70) (.15) (1 – .30) = .57
((21.13) (1 + .3461) – 21.13) (.15) (1 – .30) = .77
4 .04 / (1 – .5) = .08
(.08) (.4) / (1 – (.08) (.4)) = .0331
(5.80) (1 + .0331) = 5.99
5 ((28.44) (1 + .0331) – 28.44) (.15) (1 – .5) = .07
kc = .04 + 1.45 (.05) = .1125
kc = .04 + 1.10 (.05) = .0950
V0 = [latex]\frac{{3.22}}{{{{\left( {1 + \;.1125} \right)}^1}}}[/latex] + [latex]\frac{{4.33}}{{{{\left( {1 + \;.1125} \right)}^2}}}[/latex] + [latex]\frac{{\frac{{5.92}}{{\left( {.095\; - .0331} \right)}}}}{{{{\left( {1 + \;.1125} \right)}^2}}}[/latex] = CAD 83.67 per share
3. The growth rate cannot exceed the nominal growth rate of the economy which is normally 2.0% to 3.0% or the company will essentially become the economy over the long term, but it can be less for slow-growth, no-growth or negative-growth companies.
M. Income Approach (FCFE) at Quazar
-
Year 1
Year 2
Year 3
Year 4
EPS 5.401
6.75
8.44
8.704
Minus: (CE – D) (1 – DR) 2.312
2.89
3.61
–
Minus: Increase NWC (1 – DR) .403
.50
.63
.085
FCFE
2.69
3.36
4.20
8.62
1 .15 / (1 – .25) = .20
(.20) (1 – .0) / (1 – (.20) (1 – .0)) = .25
(4.32) (1 + .25) = 5.40
2 (3.56 – 1.10) (1 + .25) (1 – .25) = 2.31
3 ((21.23) (1 + .25) – 21.23) (.10) (1 – .25) = .40
4 .06 / (1 – .40) = .10
(.10) (.3) / (1 – (.10) (.3)) = .0309
(8.44) (1 + .0309) = 8.70
5 ((21.23) (1 + .25)3 (1 + .0309) – (21.23) (1 + .25)3) (.10) (1 – .4) = .08
P0 = [latex]\frac{{2.69}}{{{{\left( {1 + \;.1075} \right)}^1}}}[/latex] + [latex]\frac{{3.36}}{{{{\left( {1 + \;.1075} \right)}^2}}}[/latex] + [latex]\frac{{4.20}}{{{{\left( {1 + \;.1075} \right)}^3}}}[/latex] + [latex]\frac{{\frac{{8.62}}{{\left( {.0950\; - \;.0309} \right)}}}}{{{{\left( {1 + \;.1075} \right)}^3}}}[/latex] = CAD 107.26
kc = .04 + 1.35 (.05) = .1075
kc = .04 + 1.1 (.05) = .0950
N. Income Approach (FCFF) at Pulsar
1.
|
2015 |
2016 |
2017 |
|
| EBIT (1 – t)1 |
15,000 |
16,125 |
16,912 |
| Add: Non-cash charges (depreciation) |
10,000 |
10,750 |
11,275 |
| Minus: Capital expenditures2 |
18,383 |
17,038 |
15,676 |
| Minus: Increase NWC3 |
1,217 |
912 |
640 |
|
FCFF |
5,400 |
8,925 |
11,871 |
1 20,000 (1 – .25), 21,500 (1 – .25), 22,550 (1 – .25)
2 (155,283 – 136,900), (172,321 – 155,283), (187,997 – 172,321)
3 (34,223 – 22,056) – (30,800 – 19,850), (36,789 – 23,710) – (34,223 – 22,056), (38,586 – 24,867) – (36,789 – 23,710)
V0 = [latex]\frac{{5,400}}{{{{\left( {1 + \;.102} \right)}^1}}}[/latex] + [latex]\frac{{8,925}}{{{{\left( {1 + \;.102} \right)}^2}}}[/latex] + [latex]\frac{{11,871}}{{{{\left( {1 + \;.102} \right)}^3}}}[/latex] + [latex]\frac{{\frac{{\left( {11,871} \right)\left( {1 + \;.03} \right)}}{{\left( {.102 - .03} \right)}}}}{{{{\left( {1 + \;.102} \right)}^3}}}[/latex] = 148,015.65
148,015.65 x 1,000 = 148,015,650
148,015,650 – 54,250,000 + 34,750,000 = CAD 128,515,650
2.
The earnings potential of the idle land is not included in the FCFF model since the land is not currently generating income for the company. An estimate of the land’s fair value must be added to the value of the business to compensate. This would apply to the FCFE method as well.
3.
Debt instruments usually trade in secondary markets that provide reliable measures of their market value. By valuing the firm from the perspective of both debt and equity holders using the FCFF method and then deducting the market value of debt, a more accurate measure of the value of the firm to equity holders is determined. Also, the weighted average cost of capital, which is the interest rate used to discount FCFF, is generally more stable than the cost of equity used in the FCFE model thus providing a better measure of the value of the firm.
O. Income Approach (FCFF) at Wellington
1.
|
Year 0 |
Year 1 |
Year 2 |
Year 3 |
Year 4 |
Year 5 |
Year 6 |
|
| EBIT |
532.00 |
574.56 |
620.52 |
670.17 |
723.78 |
781.68 |
820.77 |
| EBIT (1-t) |
367.72 |
397.14 |
428.91 |
463.22 |
500.28 |
525.29 |
|
| Add: NCC |
223.56 |
241.44 |
260.76 |
281.62 |
304.15 |
319.36 |
|
| Minus: Net CE |
334.80 |
361.58 |
390.51 |
421.75 |
455.49 |
319.36 |
|
| Minus: Change NWC |
144.60 |
156.17 |
168.66 |
182.15 |
196.73 |
132.79 |
|
|
FCFF |
111.88 |
120.83 |
130.49 |
140.93 |
152.21 |
392.50 |
|
| Revenue |
7,230.00 |
7,808.40 |
8,433.07 |
9,107.72 |
9,836.34 |
10,623.24 |
11,154.40 |
| CE |
310.00 |
334.80 |
361.58 |
390.51 |
421.75 |
455.49 |
1319.36 |
| Depreciation |
207.00 |
223.56 |
241.44 |
260.76 |
281.62 |
304.15 |
319.36 |
| NWC |
1,807.50 |
1,952.10 |
2,108.27 |
2,276.93 |
2,459.08 |
2,655.81 |
2,788.60 |
1 Assumed in the stable-growth stage that capital expenditures and depreciation are equal.
Cost of Capital
High-Growth Stage
kc = .075 + 1.25 (.055) = .1438
WACC = (.5) (.1438) + (.5) (.095) (1 – .36) = .1023
Stable-Growth Stage
kc = .075 + 1.00 (.055) = .1300
WACC = (.75) (.13) + (.25) (.085) (1 – .36) = .1111
Value of Firm
P0 = [latex]\frac{{111.88}}{{{{\left( {1 + \;.1023} \right)}^1}}}[/latex] + [latex]\frac{{120.83}}{{{{\left( {1 + \;.1023} \right)}^2}}}[/latex] + [latex]\frac{{130.49}}{{{{\left( {1 + \;.1023} \right)}^3}}}[/latex] + [latex]\frac{{140.93}}{{{{\left( {1 + \;.1023} \right)}^4}}}[/latex] + [latex]\;\frac{{152.21}}{{{{\left( {1 + \;.1023} \right)}^5}}}[/latex]
+ [latex]\frac{{\frac{{392.50}}{{\left( {.1111\; - .05} \right)}}}}{{{{\left( {1 + \;.1023} \right)}^5}}}[/latex] = CAD 4,434.65 million
Value of Equity
4,434.65 – 2,740.58 = CAD 1,694.07 million
1,694.07 + 45 + 10 + 20 = CAD 1,769.07 million
P. Normalizing EBIT (1-t) and Net Income
Case 1 – Average Company Ratios
Net income
(ROA) (Total assets) = Net Income
(.075) (25,000,000) = 1,875,000
EBIT (1 – t)
(EBIT – (Debt) (Interest rate)) (1 – Tax rate) = Net income
(EBIT – (25,000,000) (.5) (.09)) (1 – .25) = 1,875,000
EBIT = 3,625,000
EBIT (1 – t) = 3,625,000 (1 – .25)
EBIT (1 – t) = 2,718,750
Case 2 – Average Industry Ratios
Net income
(ROE) (Total equity) = Net Income
(.085) ((60,000,000) (1-.5)) = 2,550,000
EBIT (1 – t)
(EBIT – (Debt) (Interest rate)) (1 – Tax rate) = Net income
(EBIT – ((60,000,000) (.5) (.08)) (1 – .25) = 2,550,000
EBIT = 5,800,000
EBIT (1 – t) = 5,800,000 (1 – .25)
EBIT (1 – t) = 4,350,000
Case 3 – Rating Firms
EBIT (1 – t)
3.15 = [latex]\frac{{{\rm{EBIT}}}}{{85,000,000}}[/latex]
EBIT = 267,750,000
EBIT (1 – t) = 267,750,000 (1 – .25) = 200,812,500
Net income
(EBIT – Interest expense) (1 – Tax rate) = Net income
(267,750,000 – 85,000,000) (1 – .25) = Net income
Net income = 137,062,500
Q. Income Approach (FCFF) for a Distressed Firm
1.
| Year 0 | Year 1 | Year 2 | Year 3 | Year 4 | |
| EBIT | 331 | 385 | 468 | 491 | |
| EBIT (1-t) | 248 | 288 | 351 | 368 | |
| Add: NCC | 1,132 | 1,188 | 1,248 | 1,248 | |
| Minus: Net CE | 1,297 | 1,362 | 1,430 | 1,248 | |
| Minus: Change NWC | -64 | 33 | -12 | -56 | |
| FCFF | 148 | 82 | 181 | 424 | |
| Growth rate: sales | 15.00% | 10.00% | 10.00% | 5.00% | |
| Operating profit margin | 9.00% | 9.50% | 10.50% | 10.50% | |
| Tax rate | 25.00% | 25.00% | 25.00% | 25.00% | |
| Growth rate: CE and depreciation | 5.00% | 5.00% | 5.00% | ||
| WC percentage of sales | 25.00% | 20.00% | 19.00% | 17.00% | 15.00% |
| Sales | 3,200 | 3,680 | 4,048 | 4,453 | 4,675 |
| CE | 1,235 | 1,297 | 1,362 | 1,430 | 1,248 |
| Depreciation | 1,078 | 1,132 | 1,188 | 1,248 | 1,248 |
| NWC | 800 | 736 | 769 | 757 | 701 |
| Risk-free rate | 4.00% | 4.00% | 4.00% | 4.00% | |
| Market risk premium | 5.50% | 5.50% | 5.50% | 5.50% | |
| Beta | 1.61 | 1.40 | 1.32 | 1.25 | |
| Cost of equity | 12.86% | 11.70% | 11.26% | 10.88% | |
| Cost of debt (before tax) | 9.00% | 7.50% | 7.00% | 6.00% | |
| Cost of debt (after tax) | 6.75% | 5.63% | 5.25% | 4.50% | |
| Equity weight | 55.00% | 65.00% | 70.00% | 75.00% | |
| Debt weight | 45.00% | 35.00% | 30.00% | 25.00% | |
| WACC | 10.11% | 9.57% | 9.46% | 9.28% | |
| Discount factor | 1.1011 | 1.2065 | 1.3206 |
Value of Firm
V0 = [latex]\frac{{148}}{{1.1011}}[/latex] + [latex]\frac{{82}}{{1.2065}}[/latex] + [latex]\frac{{181}}{{1.3206}}[/latex] + [latex]\frac{{\frac{{424}}{{\left( {.0928\; - .05} \right)}}}}{{1.3206}}[/latex] = CAD 7,836.02
Value of Equity
7,836.02 – 4,096.39 = CAD 3,739.63 million
R. Trailing and Leading P/E Ratios
- Trailing P/E
Last four quarters for which earnings have been reported
2011 – Q4
2012 – Q1
2012 – Q2
2012 – Q3
39.45 / 2.08 = 18.97
Last complete fiscal period
2011 – Q3
2011 – Q4
2012 – Q1
2012 – Q2
39.45 / 1.95 = 20.23
Leading P/E
Next 4 quarters including the current quarter
2013 – Q1
2013 – Q2
2013 – Q3
2013 – Q4
39.45 / 1.78 = 22.16
Next 4 quarters not including the current quarter
2013 – Q2
2013 – Q3
2013 – Q4
2014 – Q1
39.45 / 1.65 = 23.91
Next fiscal year
2013 – Q3
2013 – Q4
2014 – Q1
2014 – Q2
39.45 / 1.54 = 25.62
S. Normalizing EPS
1.
(2.17 + 1.18 + .90 + 1.19 + .57 + 1.17) / 6 = 1.20
27.45 / 1.20 = 22.88
2.
(.1270 + .1153 + .0745 + .1766 + .0855 + .1804) / 6 = .1266
(.1266) (14.29) = 1.81
27.45 / 1.81 = 15.17
3.
Historical average ROE is more accurate because it better incorporates inflation and growth of the company over the business cycle.
T. Justified Benchmark Multiples (P/E, P/S, P/BV) at Irwin
1.
Justified trailing P/E multiple
= [latex]\frac{{\left( {.750} \right)\left( {1 + \;.035} \right)}}{{.081 - \;.035}}[/latex] = 16.88
(16.88) (5.67) (100,000) = CAD 9,570,960
Justified trailing P/S multiple
= [latex]\frac{{\left( {.063} \right)\left( {.750} \right)\left( {1 + \;.035} \right)}}{{.081 - \;.035}}[/latex] = 1.06
(1.06) (86.32) (100,000) = CAD 9,149,920
Justified trailing P/BV multiple
= [latex]\frac{{\left( {.151} \right)\left( {.750} \right)\left( {1 + \;.035} \right)}}{{.081 - \;.035}}[/latex] = 2.55
(2.55) (36.54) (100,000) = CAD 9,317,700
2.
Trailing EPS and SPS could be normalized to smooth out cyclical variations, adjust for earnings manipulation, and eliminate non-recurring items. Trailing BVPS could be adjusted to included all assets and liabilities at their fair market value especially unrecognized intangible assets, goodwill, and other off-balance sheet assets and liabilities. Leading P/E and P/S multiples could also be used. All per share amounts should be expressed on a diluted basis.
3.
P/E multiple is likely the preferred multiple because it includes both the revenues and costs of the business and thus better measures its overall performance. P/S may be used if accounting manipulation is a concern and the company is in an industry where firms have similar cost structures. P/S is also easier to estimate, never negative, and more stable. P/BV is also nearly always positive, more stable, and harder to manipulate.
U. Justified Benchmark Multiple (P/E) at Hector
1.
Justified trailing P/E = [latex]\frac{{\left( {\frac{{2.56}}{{3.98}}} \right)\left( {1 + \;.035} \right)}}{{.095 - \;.035}}[/latex] = 11.10
kc = .04 + 1.1 (.05) = .095
Current P/E = [latex]\frac{{55.45}}{{3.98}}[/latex] = 13.93
Hector’s shares are overvalued as its current trailing P/E ratio is above ±5.0% of the justified trailing P/E multiple (11.10 × 1.05 = 11.65, 11.10 × .95 = 10.54). Based on the justified P/E, CAD 44.18 (11.10 x CAD 3.98) is a better estimate of the share’s intrinsic value.
2.
- This approach assumes a constant growth rate. This may be true for a mature company like Hector, but if its growth rate or other fundamental factors are expected to change over its life, using a two or three-stage model is more appropriate.
- Instead of using trailing EPS for the last year, normalized EPS may have been used. Hector is a mature firm selling a necessity so cyclical variations are not material but adjustments could be made to eliminate the effect of aggressive accounting policies and non-recurring items.
V. Justified Benchmark Multiple (P/E) for an Industry
1.
Justified trailing P/E = [latex]\frac{{\left( {1 - \;.40} \right)\left( {1 + \;.0638} \right)}}{{.10\; - \;.0638}}[/latex] = 17.63
kc = .04 + 1.2 (.05) = .10
gd = (.15) (.40) / (1 – (.15) (.40)) = .0638
17.63 × 1.05 = 18.51
17.63 × .95 = 16.75
With a current P/E ratio of 24, the industry appears to be overvalued.
2.
Many investors do not purchase individual stocks, but instead buy or sell entire industries or stock indexes based on their assessment of whether they are mispriced. The same approach as in Part 1 could be applied to a broadly-based stock index like the S&P 500. Entire industries or stock indexes can be quickly and economically purchased or sold using ETFs.
3.
Industry P/E = [latex]\frac{{{\rm{Current\;market\;value\;of\;all\;industry\;shares}}}}{{{\rm{Total\;of\;all\;industry\;trailing\;\;earnings}}}}[/latex]
4.
Industry beta is calculated by taking a weighted average of the betas of each company in the industry. The weighted average is based on each company’s market capitalization which is the number of shares times their market value. The industry retention ratio and ROE can be calculated by determining the total dividends, earnings, and equity of the industry for the last year.
5.
This approach assumes a constant growth rate. This may apply to a mature industry, but if the industry’s growth rate and other fundamental factors are expected to vary over time, using a two or three-stage model is more appropriate. If this approach was applied to a broadly-based stock index like the S&P 500, a one-stage model would be appropriate as the fundamentals would likely remain constant.
W. Justified Benchmark Multiple (P/E) Using a 2-Stage Model at Dixon
1.
[latex]\frac{{{{\rm{P}}_0}}}{{{{\rm{E}}_0}}}[/latex] = [latex]\frac{{\left( {.40} \right){{\left( {1 + .191} \right)}^1}}}{{{{\left( {1 + .105} \right)}^1}}}[/latex] + [latex]\frac{{\left( {.40} \right){{\left( {1 + .191} \right)}^2}}}{{{{\left( {1 + .105} \right)}^2}}}[/latex] + [latex]\frac{{\left( {.40} \right){{\left( {1 + .191} \right)}^3}}}{{{{\left( {1 + .105} \right)}^3}}}[/latex] + [latex]\frac{{\frac{{\left( {.70} \right){{\left( {1 + .191} \right)}^3}\left( {1 + .039} \right)}}{{\left( {.095 - .039} \right)}}}}{{{{\left( {1 + .105} \right)}^3}}}[/latex] = 17.66
(17.66) (5.10) = CAD 90.07
High-Growth Stage
.04 + 1.3 (.05) = .105
(.16 / (1 – .40)) = .267
(.267) (1 – .40) / (1 – (.267) (1 – .40)) = .191
Stable-Growth Stage
.04 + 1.1 (.05) = .095
.05 / (1 – .60) = .125
(.125) (1 – .70) / (1 – (.125) (1 – .70)) = .039
X. Market Multiples Approach (P/E) at Hi-tech
1.
(14.29 + 16.17 + 16.08 + 14.77 + 15.48 + 18.16) / 6 = 15.82
Based on Trailing EPS
P0 = (15.82) (4.51) = CAD 71.35
Based on Leading EPS
P0 = (15.82) (3.51) = CAD 55.53
Hi-tech’s common shares which currently trade at CAD 56.48 appear to be fairly valued based on leading EPS which reflects the effect of product delays on earnings. Jackson may still decide that Hi-tech’s shares are undervalued if she feels the decline in EPS is a one-time event and that EPS will return to previous levels after 2016 once the product delays are addressed.
2.
- 12-month Leading EPS could have been used instead of the 12-month trailing EPS to calculate the sub-industry average P/E ratio since it is a forward-looking measure.
- Normalized trailing EPS for the last business cycle could be used to average out the effects of any economic fluctuations on earnings for each of the companies in the sub-industry and Hi-tech. Normalization requires data for a full business cycle, so trailing EPS is generally used since leading EPS is only available for a limited number of periods in the future.
Y. Market Multiples Approach (P/BV) at Ballantyne
1.
(1.96) (25) = 49
(49) (10,000,000) = CAD 490,000,000
2.
BVPS for the comparable sub-industry companies and Ballantyne may be re-stated to include all assets and liabilities at fair value. This is a time-consuming process, so it may not be done. Greater use of fair value accounting under IFRS will produce better measures of BVPS.
Also, using median instead of a mean or average sub-industry P/BV multiple may help reduce the effect of statistical outliers.
Z. Market Multiples Approach (P/E) at Regal
1.
|
Company |
Price ($) |
Normalized Trailing EPS |
P/E |
| ABC |
56.67 |
3.14 |
18.05 |
| ACME |
45.91 |
2.09 |
21.97 |
| Widgets |
23.56 |
1.68 |
14.02 |
| Bloggins |
44.78 |
2.99 |
14.98 |
|
Comparable Mean |
17.26 | ||
Average EPS
(5.10 + 4.21 + 2.34 + 1.67 + 2.55 + 3.21) / 6 = 3.18
Average ROE
(27.50 + 20.10 + 14.56 + 5.60 + 12.45 + 16.67) / 6 = 16.15
(.1615) (18.56) = 3.00
Regal
Average EPS = 35.56 / 3.18 = 11.18
Average ROE = 35.56 / 3.00 = 11.85
Recommendation
Buy Regal as its P/E is well below the peer group average of 17.26 under both approaches for calculating normalized trailing EPS. It is currently valued at CAD 35.56, but a more appropriate value may be CAD 51.78 (17.26 X CAD 3.00). CAD 3.00 was used instead of CAD 3.18 because it was calculated using average ROE ratios instead of average EPS.
3. Normalizing EPS helps to even out cyclical variations in earnings over a business cycle.
4.
- Comparable companies may not be very similar to Regal even though they are in the same sub-industry.
- Sample size of only four companies may be insufficient to establish a reliable estimate.
- There could be good reason for Regal’s lower P/E such as higher risk or lower growth, so its share price may not move towards the peer group average P/E over time.
AA. Market Multiples Approach (P/E) at Horizon
1.
| Gaggle | 193.18 / 24 |
8.05 |
| Cosmos | 364.86 / 35 |
10.42 |
| Navigator | 90.91 / 15 |
6.06 |
| Laurentian | 102.42 / 18 |
5.69 |
| Tech Smart | 688.89 / 45 |
15.31 |
| Dream Quest | 10.50 / 9 |
1.17 |
|
Comparable mean |
7.78 | |
The market is paying the least for growth at Dream Quest, Laurentian, and Navigator.
Dream Quest is recommended unless further investigation into its risk level (beta) and an analysis of its financial statements indicates a reason for this low price for growth. Investors may have gotten caught up in the excitement of the higher growth at Dream Quest’s competitors causing its share to be neglected resulting in a lower PEG ratio. This is a market inefficiency that investors should exploit to earn alpha.
BB. Market Multiples Approach (P/E) at Maple Leaf
1.
CGR, MFF, NRM as their trailing and leading P/E are below the sub-industry mean/median.
2.
Median will eliminate the influence of outlying values, but in this case the two measures of central tendency are close in value.
3.
The P/E ratio of a company may be low for a good reason. The factors that influence P/E must be considered:
Risk (as measured by beta) ↑ – P/E ↓
Growth ↑ – P/E ↑
Before recommending the company, further analysis should be done to determine if differences in risk or growth for CGR, MFF, or NRM can explain the low P/E.
4.
Beta is the same for CGR and MFF and is below the sub-industry mean or median. NRM’s beta is above the industry mean or median.
Growth varies considerably, so the PEG ratio should be used to assess the influence of growth. CGR and MFF are charging the least for growth (2.04 and 2.14), and they also have the lowest betas. These two shares should be recommended.
CC. Market Multiples Approach (P/S) at RRJ
1.
| Company | P/S/G | Profit Margin (%) | Forecasted Profit Margin (%) | Beta | ||
| Closing Price | YTD High |
YTD Low |
||||
| Evert Enterprises |
.033 |
.043 |
.025 |
3.60 |
3.00 |
1.13 |
| Divers Consolidated |
.048 |
.055 |
.027 |
2.64 |
3.12 |
1.28 |
| Canmore Industries |
.038 |
.058 |
.032 |
3.50 |
3.75 |
.93 |
Canmore is the best value investment. Divers is near its yearly high for P/S/G and will not likely rise much further. Evert and Canmore are near their yearly lows for P/S/G so these shares have good potential as value investments. Canmore’s profits are expected to rise more than either Evert or Divers and their risk is the lowest of the three competitors, so they have the most upward potential.
DD. Market Multiples Approach (P/BV) at Surefire
1.
Pearle
|
Share |
P/BV / 5-Year Average |
P/BV / Industry |
Beta / Industry |
ROE / Industry |
|
Pearle |
.92 |
.78 |
.917 |
.97 |
|
Jasmin |
1.16 |
.81 |
1.00 |
.77 |
|
Diamond |
.87 |
.53 |
1.33 |
.65 |
|
Gold |
1.06 |
.70 |
1.00 |
.81 |
For both Pearl and Diamond, the current P/BV is below the 5-year average and the current industry average. Diamond’s P/BV is trending up slowly, but has taken a recent dip which could make it a good value candidate. Diamond seems to be below for good reason though due to its high risk and low ROE. Based on this uncertainty, it is not recommended. Pearle’s P/BV is trending down, but has recently experienced a significant reversal in this trend. This combined with Pearle’s high ROE and low beta would indicate good prospects for short-term gains.
2.
The industry mean may have been selected instead of the comparable company mean because of the small number of comparable companies available. Also, analysts may believe that this sub-industry is mis-valued and that a comparison with the larger industry, industry group, or sector will provide a more accurate valuation.
3.
Cross-sectional regression could be used to incorporate all fundamentals (ROE, beta, payout, growth) in a less subjective, more quantitative manner.
EE. Market Multiples Approach (P/E) at Astro
1.
Random
Current P/E = 14.67
Historical average compared to the market – (.95) (19.2) = 18.24
Housley
Current P/E = 27.33
Historical average compared to the market – (1.23) (19.2) = 23.62
Backtrack
Current P/E = 15.31
Historical average compared to the market – (1.11) (19.2) = 21.31
Both Random and Backtrack are undervalued with Backtrack displaying the greatest potential for profit.
4. Using P/E ratios of the larger industry, industry group, sector or the stock market as a whole can provide confirmation that the smaller sub-industry markets are being priced efficiently. Occasionally, these groups can become mispriced as shown in the internet bubble in the early 2000s.
FF. Market Multiples Approach (P/E) using Multi-Regression at Timmins
1.
P/E = 13.05 + 2.34 (.50) – .31 (1.1) + 15.23 (.07) = 14.95
The company currently has a trailing P/E multiple of 17.5 so it is probably overvalued and should not be purchased or sold.
2.
The P/E multiple based on sub-industry data is adjusted for differences in the risk, growth and payout factors.
3.
Statistical problems
- The sample size of eight company is small. If possible, expand the number of companies in the peer group, but this may be difficult if there are a large number of private companies. It may be necessary to go beyond the sub-industry to increase the same size which will make the comparison companies less comparable.
- R2 of .89 is high this year, but this value will likely change significantly from year to year.
- There could be multi-collinearity between some of the independent variables which can make the coefficients less stable over time and have incorrect signs (no logically cause and effect relationship). Analysts could produce a cross tabulation of the independent variables and see if they are highly correlated with each other. If they are, consider dropping one of the highly correlated variables.
- The t-stats or p-values for each coefficient may not be statistically significant. This may be a good factor to eliminate if multi-collinearity is present.
- The size of the factor (coefficient times value) may be small. Again, this may be a good factor to eliminate if multi-collinearity is present.
GG. Market Multiples Approach (P/E) using Multi-Regression at Shamrock
1.
Hanson, Flagstaff, Hinton Park, Stinson
Note: Due to potential statistical errors, stocks were only listed as undervalued if the current P/E was below the sub-industry average P/E by at least 1.
2.
The P/E based on sub-industry data is not adjusted for differences in the risk, growth and payout factors.
3.
P/E = -2.43591 + .3574 (EGR) + 11.9688 (Beta) + .0290 (Payout)
Regression Results
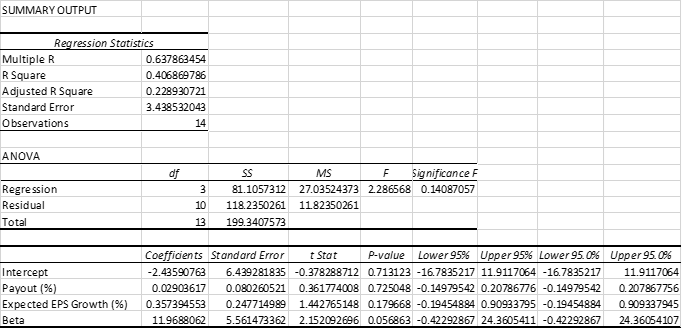
Multicollinearity Table

4.
Statistical concerns
- R2 is low and standard error is high. R2 values of 80% to 90% are not uncommon in some years.
- The t-stat is very low for the payout factor and low for the expected growth so they are not statistically significant.
- Beta normally has a negative coefficient as increased risk generally lowers the P/E.
- Does not appear to be any problems with multi-collinearity based on the cross tabulation.
Overall, this model is not very strong this year and has statistical errors. Inconsistency in the strength of the model from one year to the next is one of the problems of the approach.
5.
Using the model in Part 3, the following predicted P/E’s were calculated:
|
Company |
Current P/E |
Predicted P/E |
| Harrison Industries |
18.1 |
13.5 |
| Churchill Ltd. |
16.2 |
18.7 |
| Emerson Consolidated |
17.2 |
14.3 |
| Osgood Enterprises |
11.9 |
12.6 |
| Hanson Inc. |
10.7 |
12.9 |
| Smithson Ltd. |
13.0 |
13.8 |
| Donner Sisters |
13.9 |
13.8 |
| Flagstaff Enterprises |
11.5 |
11.9 |
| Jenkins Brothers |
23.6 |
17.9 |
| Hinton Park Industries |
9.9 |
15.5 |
| Killarney Inc. |
12.6 |
11.3 |
| Emerson Group |
14.5 |
15.5 |
| Stinson Ltd. |
9.1 |
12.0 |
| Lively Inc. |
10.9 |
9.5 |
Churchill, Hanson, Hinton Park, Stinson
Note: Due to potential statistical errors, stocks were only listed as undervalued if the predicted P/E was greater than the current P/E by at least 1.
HH. Market Multiples Approach (P/E) using Multi-Regression at Wainwright
1.
P/E = 17.45 + .0654 (.15) – .612 (.92) + .512 (.20) = 17.00
(17.00) (15,000,000) = CAD 255,000,000
Forward-looking expected growth rate – 15%
Beta
Industry average beta was de-levered to match the client company’s financing structure.
1.21 = Bu (1 + (1 – .25) (.4285))
D/E = .3 / (1 – .3) = .4285
Bu = .92
Dividend payout
The company does not pay dividends, so they were estimated using FCFE.
FCFE = 15 – 18 + 7 – 1 = 3
Payout ratio = 3 / 15 = 20%
II. Market Multiples Approach (P/E) at Lancaster
1.
(14.00 + 15.40 + 17.92 + 15.54 + 13.58) / 5 = 15.29
Based on Trailing EPS
P0 = (15.29) (4.10) = CAD 62.69
Based on Leading EPS
P0 = (15.29) (4.35) = CAD 66.51
Lancaster’s share which currently trade at CAD 52.44 appears to be undervalued based on both trailing and leading EPS. Leading EPS likely provides the best estimate of the share’s fair value since it is forward looking.
2.
This approach may be used if reliable market data is not available for comparable companies. This method should not be used if a firm’s business mix or level of financial or operational leverage has been altered as past data will not be representative of future performance.
JJ. Market Multiples Approach (EV/FCFF) at Sunshine
1.
|
Soul Shoes |
Bulldog |
Trail Rider |
|
| Market value equity |
9,560 |
16,560 |
43,230 |
| Market value debt |
7,030 |
9,030 |
18,670 |
| Cash and marketable securities |
3,850 |
1,890 |
1,210 |
| EV1 |
12,740 |
23,700 |
60,690 |
| EBIT |
4,252 |
4,745 |
11,749 |
| Depreciation and Amortization |
2,950 |
3,163 |
7,230 |
| Capital expenditures |
3,370 |
3,954 |
9,038 |
| Change in working capital |
1,080 |
1,340 |
2,860 |
| FCFF2 |
1,689 |
1,428 |
4,144 |
| EV/FCFF |
7.54 |
16.60 |
14.64 |
| Beta |
1.2 |
1.3 |
1.1 |
| Growth rate |
5.2% |
6.1% |
5.3% |
1Market value equity + Market value of debt – Cash and marketable securities
2EBIT (1-TR) + NCC – CE – ΔNWC
Soul Shoes is a strong candidate for inclusion in Sunshine’s value fund. Its EV/FCFF ratio is well below the other two companies and there does not appear to be any justification for it. Soul’s beta and growth rate are very similar to its two competitors. In the short term, the share price should increase and bring the EV/FCFF in line with the industry.
2. Analysts find the EV/FCFF approach useful when analyzing companies with significant differences in their use of financial leverage and capital intensity. EV/FCFF is preferable to EV/EBITDA because FCFF measures all cash flow available to both debt and equity investors.
KK. Market Multiples Approach (EV/FCFF) at Ashton
1.
(25.3) (1 – .25) + 5.3 – 7.40 – .85 = 16.02
(16.02) (12.3) – 59.20 = 137.85
The value of the firm is estimated to be CAD 137.85 million.
2.
The forest products industry is cyclical so it recommended that FCFF be normalized over one full business cycle allowing for both inflation and growth. FCFF should be normalized for all companies used to calculate the forest products sub-industry average EV/FCFF. Ashton’s FCFF should also be normalized for one full business cycle using company or industry average ratios or rating firm ratios if warranted.
LL. Asset-Based Approach at Willington
1.
| Cash |
17,780 |
| Temporary investments1 |
64,801 |
| Accounts receivable2 |
47,612 |
| Notes receivable3 |
33,250 |
| Inventory4 |
315,000 |
| Equipment |
950,000 |
| Building |
210,000 |
| Land under lease5 |
129,748 |
| Government license |
58,000 |
| Total Assets |
1,826,191 |
| Accounts payable6 |
207,375 |
| Line of credit7 |
100,000 |
| Contingent liability |
50,000 |
| Term loan8 |
399,831 |
| Obligation under capital lease5 |
129,748 |
| Total liabilities |
886,954 |
1 [latex]\frac{{64,828{\rm{\;}}{{\left( {1 + {\rm{\;}}\frac{{.025}}{{12}}} \right)}^2}}}{{{{\left( {1 + {\rm{\;}}\frac{{.0275}}{{12}}} \right)}^2}}}[/latex]
2 [latex]\frac{{48,000}}{{{{\left( {1 + \;\frac{{.0325}}{{12}}} \right)}^3}}}[/latex]
3 Future value and present value cancel each other out
4 (350,000) (1 – .10)
5 10,000 [latex](\frac{{1 - {{\left( {1 + \;.075} \right)}^{ - 50}}}}{{.075}}[/latex])
6 [latex]\frac{{208,500}}{{{{\left( {1 + \;\frac{{.0325}}{{12}}} \right)}^2}}}[/latex]
7 Future value and present value cancel each other out
8 4,540 [latex](\frac{{1 - {{\left( {1 + \;\frac{{.065}}{{12}}} \right)}^{ - 120}}}}{{\left( {\frac{{.065}}{{12}}} \right)}}[/latex])
| Net assets (1,826,191 – 207,375 – 100,000 – 50,000) | 1,468,816 |
| Times: Weighted average cost of capital (9.50%) | .0950 |
| Required level of income | 139,538 |
| Free cash flow to the firm | 162,944 |
| Minus: Normal or required level of income | 139,538 |
| Excess earnings per year | 23,406 |
1 Accounts payable, line of credit, and contingent liability are deducted from total assets to give net working capital. Net assets consist of long-term assets plus net working capital.
Goodwill
[latex]\frac{{23,406}}{{.0950 - \;.03}}[/latex] = 360,092
Note that in this solution, excess profits are assumed to continue forever and to grow at 3% per year. This is an example of a growing perpetuity. While the assumption that excess profits would continue forever is explicit in the question, it is up to the evaluator (the student) to assess whether to include growth in their estimate. In the next problem, Problem MM: Asset-Based Approach at Ambrose, it is explicitly stated that excess profits would continue for only 5 years, and, as in this problem, it is left to the student to determine whether to assume the excess profits will grow. In the solution to Problem MM: Asset-Based Approach at Ambrose, it is assumed that the excess profits will not grow. This is an example of an ordinary annuity. Had it been assumed that the excess profits would grow for the 5 years, it would be a growing annuity.
Business Valuation
(1,826,191 – 207,375 – 100,000 – 50,000) + 360,092 – 399,831 – 129,748 = 1,229,329
The common equity of Willington has an intrinsic value of CAD 1,229,329.
MM. Asset-Based Approach at Ambrose
1.
| Cash |
9,980 |
| Accounts receivable 1 |
34,623 |
| Inventory 2 |
18,525 |
| Land under capital lease 3 |
26,803 |
| Building |
65,000 |
| Equipment |
32,500 |
| Other assets |
57,500 |
| Total Assets |
244,931 |
| Accounts payable 4 |
53,441 |
| Long-term debt 5 |
54,400 |
| Obligation under capital lease 3 |
26,803 |
| Total liabilities |
134,644 |
1 [latex]\frac{{35,000}}{{{{\left( {1 + {\rm{\;}}\frac{{.0325}}{{12}}} \right)}^4}}}[/latex]
2 (19,500) (1 – .05)
3 (2,300,000) [latex](\frac{{1 - {{\left( {1 + \;.07} \right)}^{ - 25}}}}{{.07}}[/latex])
4 [latex]\frac{{53,740}}{{{{\left( {1 + {\rm{\;}}\frac{{.0335}}{{12}}} \right)}^2}}}[/latex]
5 Future value and present value cancel each other out (2,930 + 51,470)
| Net assets (244,931 – 53,441) |
191,490 |
| Times: Weighted average cost of capital (10.5%) |
.105 |
| Normal or required level of income |
20,106 |
| Free cash flow to the firm |
25,000 |
| Minus: Normal or required level of income |
20,106 |
| Excess earnings per year |
4,894 |
Goodwill
= [latex]\frac{{4,894}}{{{{\left( {1 + \;.105} \right)}^1}}}[/latex] + [latex]\frac{{4,894}}{{{{\left( {1 + \;.105} \right)}^2}}}[/latex] + [latex]\frac{{4,894}}{{{{\left( {1 + \;.105} \right)}^3}}}[/latex] + [latex]\frac{{4,894}}{{{{\left( {1 + \;.105} \right)}^4}}}[/latex] + [latex]\frac{{4,894}}{{{{\left( {1 + \;.105} \right)}^5}}}[/latex] = 18,318
Business Valuation
(244,931 – 53,441) + 18,318 – 54,400 – 26,803 = 128,605
The common equity of Ambrose has an intrinsic value of CAD 128,605,000.
NN. Residual Income Approach at High Mountain
1.
Vo =47.98 + [latex]\frac{{0.102\; - \;0.082}}{{0.082 - 0.035\;}}\;\left( {47.98} \right)[/latex] = CAD 68.40
Yes, it appears that the company is a good investment. It currently trades at CAD 53.42 but the share has an intrinsic value of CAD 68.40.
2.
The long-term rate of return on equity (ROE) is 10.2% which well exceeds the required rate of return (RRR) of 8.2%. Excess return will attract new companies to the industry increasing competition and lowering the ROE. It is unreasonably to assume that excess returns will last indefinitely. This problem can be addressed by using a 2-stage or 3-stage approach that allows the ROE to remain above the RRR for period of time before reverting to the RRR. The long-term growth rate of 3.5% approximates the long-term growth rate of the economy so it is suitable for a 1-stage model. With a 2-stage or 3-stage model, a higher growth rate could be used in the initial periods before it reverts to the long-term growth rate of the economy.
OO. Residual Income Approach at Majestic
1.
|
Year |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| ROA | 17.00% | 17.00% | 17.00% | 17.00% | 17.00% | 15.08% | 13.17% | 11.25% | 9.33% | 7.42% | 5.50% |
| Payout ratio | 30.00% | 30.00% | 30.00% | 30.00% | 30.00% | 37.50% | 45.00% | 52.50% | 60.00% | 67.50% | 75.00% |
| Debt ratio | 20.00% | 20.00% | 20.00% | 20.00% | 20.00% | 23.33% | 26.67% | 30.00% | 33.33% | 36.67% | 40.00% |
| Beta | 1.30 | 1.30 | 1.30 | 1.30 | 1.30 | 1.27 | 1.23 | 1.20 | 1.17 | 1.13 | 1.10 |
| RFR | 4.00% | 4.00% | 4.00% | 4.00% | 4.00% | 4.00% | 4.00% | 4.00% | 4.00% | 4.00% | 4.00% |
| MRP | 5.00% | 5.00% | 5.00% | 5.00% | 5.00% | 5.00% | 5.00% | 5.00% | 5.00% | 5.00% | 5.00% |
| RRR | 10.50% | 10.50% | 10.50% | 10.50% | 10.50% | 10.33% | 10.17% | 10.00% | 9.83% | 9.67% | 9.50% |
| ROE | 21.25% | 21.25% | 21.25% | 21.25% | 21.25% | 19.67% | 17.95% | 16.07% | 14.00% | 11.71% | 9.17% |
| Growth in BVPS | 17.47% | 17.47% | 17.47% | 17.47% | 17.47% | 14.02% | 10.96% | 8.26% | 5.93% | 3.96% | 2.35% |
| ROE – RRR | 10.75% | 10.75% | 10.75% | 10.75% | 10.75% | 9.34% | 7.79% | 6.07% | 4.17% | 2.04% | -0.33% |
| BVPS | 9.93 | 11.66 | 13.70 | 16.09 | 18.90 | 21.56 | 23.92 | 25.89 | 27.43 | 28.52 | 29.18 |
| RI | 1.07 | 1.25 | 1.47 | 1.73 | 2.03 | 2.01 | 1.86 | 1.57 | 1.14 | 0.58 | (0.10) |
| Discount factor | 1.1050 | 1.2210 | 1.3492 | 1.4909 | 1.6474 | 1.8177 | 2.0025 | 2.2027 | 2.4193 | 2.6532 | 2.9053 |
| PV RI | 0.97 | 1.03 | 1.09 | 1.16 | 1.23 | 1.11 | 0.93 | 0.71 | 0.47 | 0.22 | (0.03) |
| Intrinsic Value 1 | 17.37 |
1 Intrinsic value = Current BVPS + Sum of PV RI
PP. Marketability Discounts at Adirondack
1.
85,000,000 (1 – .4) = 51,000,000
The company’s estimated value of CAD 85,000,000 is based on its current earnings which still reflect the issues relating to excessive salaries, hiring of family members, personal use of company assets, sub-optimal leverage and inventory management. These inefficiencies will likely continue if Adirondack remains private. The estimated value of the company includes the costs of not having control, so a non-control discount was not applied. The marketability discount is quite large at Adirondack reflecting the high cost of selling private company shares and weaker shareholder rights.
2.
105,000,000 (1 – .05) = 99,750,000
The company’s estimated value of CAD 105,000,000 is based on normalized earnings which will be higher after addressing operational issues relating to excessive salaries, hiring of family members, personal use of company assets, sub-optimal leverage and inventory management. If Adirondack goes public, it is much more likely that these issues will be dealt with by a new board of directors, more professional management, and increased investor scrutiny.
The benefits of having control are included in the higher estimated value of the company so a control premium was not applied. The marketability discount is small as Phillips has committed to becoming a public company but there is still some concern as to whether the transaction will occur. Also, Adirondack will still be a small public business and thus less marketable in the public markets compared to larger firms.
3.
Phillips has abused the rights of the minority shareholders which has contributed to the large marketability discount. It will be difficult given Phillip’s ownership position and the weak shareholder agreement, but the individual investors should lobby for greater rights and accountability. Some actions may include:
- Ensure the board of directors has members who are selected by the minority investors.
- Establish regular meeting times and quorum rules for the board of directors and dismiss board members who do not attend regularly or are unprepared.
- Establish active board committees especially audit, compensation, personnel.
- Have the board of directors review all major decisions and require supermajority support.
- Secure more professional management and reduce the company’s dependency on Phillips.
- Provide financial information on a regular basis and require audits.
- Pay larger dividends on a regular basis to reward shareholders and encourage better management.
- Make any restrictions on the sale of shares more favorable to minority investors including rights of first refusal, piggy-back rights, pre-emptive rights.
QQ. Valuing a Private Company at Adams River
1.
FCFE = 11.8 – (.1726) (1 – .25) – (1.381) (1 – .25) = 10.635
Growth in Revenue
(X) (1 + .034) = 210 X = 203.095
(210 – 203.095) = 6.905
Capital Expenditures minus Depreciation and Amortization
(6.905) (.25) = 1.726
1.726 – (1.726) (.90) = .1726
Working Capital
(6.905) (.20) = 1.381
Cost of Equity
.04 + .05 + .03 + .01 + .01 = .14
FCFE Model
[latex]\frac{{\left( {10.635} \right)\left( {1 + \;.034} \right)}}{{.14 - \;.034}}[/latex] = 103.741
103.741 (1 – .20) = 82.993
Adams River as a privately-held company from the perspective of the minority interest is worth approximately CAD 82.993 million. Normalized income was not used because if the company remains private, the controlling owner will not likely make the changes identified. Net income was used and it does not include the benefits of control, so a non-control discount was not required. As a private company, the marketability discount was applied.
2.
FCFE = 12.775 – (.1726) (1 – .25) – (1.381) (1 – .25) = 11.610
Normalization of Net Income
11,800,000 + (1,800,000 – 800,000) (1 – .25) + (300,000) (1 – .25) = 12,775,000
FCFE Model
[latex]\frac{{\left( {11.610} \right)\left( {1 + \;.034} \right)}}{{.14 - \;.034}}[/latex] = 113.252
Adams River as a public company from the perspective of the minority interest is worth approximately CAD 113.252 million. If the company is taken public, new management will likely address the issues identified. The higher normalized income amount is used to reflect the benefits of control and no marketability discount was applied as the shares will trade publicly.
RR. Valuing a Private Company at Dawson Falls
1.
| Gross profit | 190 million x .45 | 85.5 million |
| Selling and administration | 190 million x .20 | 38.0 million |
| Depreciation | 190 million x .05 | 9.5 million |
| EBIT | 38.0 million |
FCFF = (38.0) (1 – .25) + (9.5) – (11.221) – (.642) = 26.137
(26.137) (1 + .035) (10.32) = 279.17
279.17 – 105.30 = 173.87
Growth in Revenue
(X) (1 + .035) = 190 X = 183.575
(190 – 183.575) = 6.425
Capital Expenditures
(9.5) (1.10) + (6.425) (.12) = 11.221
Working Capital
(6.425) (.10) = .642
2.
(173.87) (1 – .20) (1 – .25) = 104.32
3.
Guideline private transactions were selected because they are for control acquisitions only and, therefore, include all the benefits of control. They are useful for valuing control interests like with Dawson Falls in Part 1. For minority interests, a non-control discount along with a marketability discount will have to be applied as in Part 2.
The problem with this approach is that the number of transactions of this type are limited and as a result some older transactions may have to be used. The multiples in these older transactions are not representative of the current market and may lead to a faulty valuation. Also, no adjustments are made for the varying business fundamentals of the companies involved.
A better approach might be to use guideline public companies from the sub-industry as pure plays. The comparison companies are readily available, the information is recent, and adjustment can be made for varying business fundamentals. The problem is that data from public companies does not include the benefits of control so this will have to be added using a control premium.

